【2025刷题笔记】- 两个字符串间的最短路径问题
刷题笔记合集🔗
两个字符串间的最短路径问题
问题描述
给定两个字符串,分别为字符串 A 与字符串 B。
例如 A 字符串为 "ABCABBA",B 字符串为 "CBABAC" 可以得到下图 的二维数组,定义原点为
,终点为
,水平与垂直的每一条边距离为 1,映射成坐标系如下图。
从原点 到
为水平边,距离为 1,从
到
为垂直边,距离为 1;
假设两个字符串同一位置的两个字符相同,则可以作一个斜边,如 到
最短距离为斜边,距离同样为 1。
作出所有的斜边如下图, 到
的距离为:1 个水平边 + 1 个垂直边 + 1 个斜边 = 3。
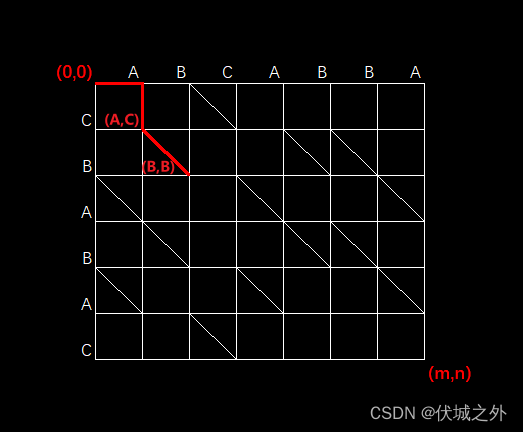
根据定义可知,原点到终点的最短距离路径如下图红线标记,最短距离为 9:

输入格式
输入的唯一一行包含空格分割的两个字符串 A 与字符串 B。
- 字符串不为"空串"
- 字符格式满足正则规则:[A-Z]
- 字符串长度
输出格式
输出的唯一一行包含一个整数,表示原点到终点的最短距离。
样例输入
ABC ABC
ABCABBA CBABAC
样例输出
3
9
| 样例 | 解释说明 |
|---|---|
| 样例1 | 两个字符串"ABC ABC"完全相同,从原点到终点的最短路径是沿对角线行走,长度为3。 |
| 样例2 | 按照题目示例图,A="ABCABBA",B="CBABAC",原点到终点的最短路径长度为9。 |
数据范围
- 字符串不为"空串"
- 字符格式满足正则规则:[A-Z]
- 字符串长度
题解
这个问题可以看作是寻找两个字符串之间的最短编辑路径,与经典的动态规划问题有些相似,但规则有所不同。
问题理解
首先理解题目建立的模型:
- 我们有两个字符串A和B,形成一个二维网格
- 从起点(0,0)到终点(m,n),其中m是B的长度,n是A的长度
- 可以水平、垂直或斜对角线移动,每种移动的距离都是1
- 当且仅当两个字符串在对应位置的字符相同时,才能走斜对角线
实际上,这个问题本质上是在寻找一条从起点到终点的最短路径,同时还能利用字符相同时的"捷径"(斜对角线)。
动态规划解法
我们可以使用动态规划来解决这个问题:
- 定义状态:dp[i][j]表示从原点(0,0)到点(i,j)的最短距离
- 状态转移方程:
- 如果A[j-1] == B[i-1](字符相同),则可以走斜线:dp[i][j] = dp[i-1][j-1] + 1
- 否则,只能水平或垂直移动:dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + 1
- 边界条件:
- dp[0][j] = j,表示从(0,0)到(0,j)的距离是j(j步水平移动)
- dp[i][0] = i,表示从(0,0)到(i,0)的距离是i(i步垂直移动)
优化:空间压缩
由于dp[i][j]只依赖于dp[i-1][j-1]、dp[i-1][j]和dp[i][j-1],所以我们只需要保存当前行和前一行的dp值即可,不需要存储整个dp矩阵。
这种优化方法将空间复杂度从O(m*n)降低到O(n),这对于长字符串来说非常重要,能避免内存溢出问题。
时间和空间复杂度
- 时间复杂度:O(m*n),其中m和n分别是两个字符串的长度
- 空间复杂度:使用优化后的方法是O(n),不使用优化是O(m*n)
对于题目给出的约束(字符串长度<10000),优化的空间复杂度对于避免内存限制非常重要。
参考代码
- Python
import sys
input = lambda:sys.stdin.readline().strip()
# 输入获取
A, B = input().split()
m, n = len(B), len(A)
# 计算从原点到终点的最短路径长度
def find_shortest_path():
# 使用空间压缩的动态规划
# prev_row存储上一行的dp值
prev_row = list(range(n + 1))
# 当前行的dp值
curr_row = [0] * (n + 1)
for i in range(1, m + 1):
# 第一列的值等于行索引(垂直距离)
curr_row[0] = i
for j in range(1, n + 1):
if A[j-1] == B[i剩余60%内容,订阅专栏后可继续查看/也可单篇购买
本专栏收集并整理了一些刷题笔记
 查看8道真题和解析
查看8道真题和解析