逆元（分数取模）
及ax=1(modn) 求解x（称为a关于模p的乘法逆元）
分析有： 原式等价于ax-1=yn, 求解x,y; 及exgcd(x,y) 并且gcd(x,y)=1 也就是互质时有解；
exgcd求逆元代码：
void exgcd(int a,int b,int &d,int &x,int &y){
if(!b){
d=a;
x=1，y=0;
}
else {
gcd(b,a%b,d,y,x);
y-=x*(a/b);
}
} 费马小定理求逆元（前提m是质素的，且a不是m的倍数）：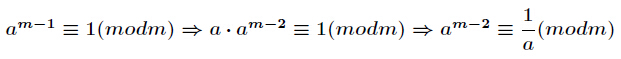
所以 
就是a关于模m的逆元；然后快速幂
对于分数的形式 a/b(mod m) 因为b*b^(m-2)=1(mod m) 所以 a/b==a/b*(b*b^(m-2)) ==a*b^(m-2) (mod m)
还一个方法
当p是个质数的时候有
inv(a) = (p - p / a) * inv(p % a) % p
证明：
设x = p % a,y = p / a
于是有 x + y * a = p
(x + y * a) % p = 0
移项得 x % p = (-y) * a % p
x * inv(a) % p = (-y) % p
inv(a) = (p - y) * inv(x) % p
于是 inv(a) = (p - p / a) * inv(p % a) % p
然后一直递归到1为止，因为1的逆元就是1
以后去养老公司吧