【2025刷题笔记】- 二维伞的雨滴效应
刷题笔记合集🔗
二维伞的雨滴效应
问题描述
普通的伞在二维平面世界中,左右两侧均有一条边,而两侧伞边最下面各有一个伞坠子,雨滴落到伞面,逐步流到伞坠处,会将伞坠的信息携带并落到地面,随着日积月累,地面会呈现伞坠的信息。
1、为了模拟伞状雨滴效应,用二叉树来模拟二维平面伞(如下图所示),现在输入一串正整数数组序列(不含0,数组成员至少是1个),若此数组序列是二叉搜索树的前序遍历的结果,那么请输出一个返回值1,否则输出0。
2、同时请将此序列构成的伞状效应携带到地面的数字信息输出来(左边伞坠信息,右边伞坠信息,详细参考示例图地面上数字),若此树不存在左或右扇坠,则对应位置返回0。同时若非二叉排序树那么左右伞坠信息也返回0。
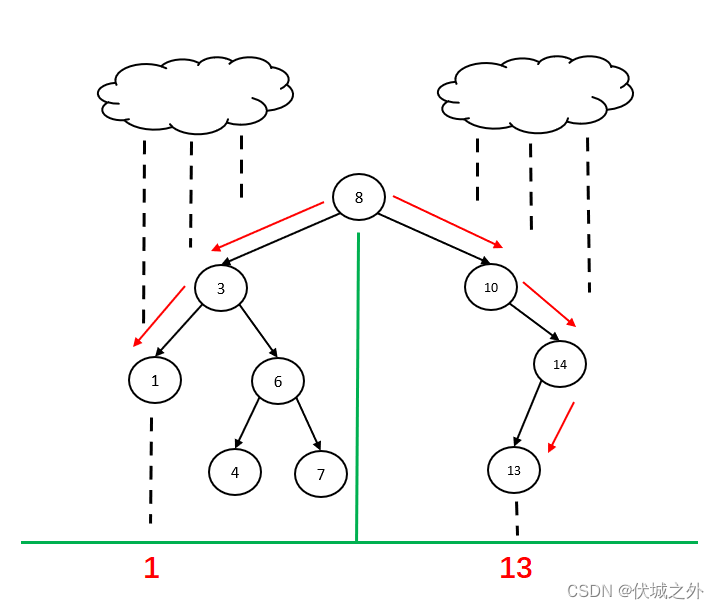
输入格式
一个通过空格分割的整数序列字符串,数组不含0,数组成员至少1个,输入的数组的任意两个数字都互不相同,最多1000个正整数,正整数值范围1~65535。
输出格式
输出如下三个值,以空格分隔:是否二叉排序树,左侧地面呈现的伞坠数字值,右侧地面呈现的伞坠数字值。
若是二叉排序树,则输出1,否则输出0(其左右伞坠值也直接赋值0)。
若不存在左侧或者右侧伞坠值,那么对应伞坠值直接赋值0。
样例输入
8 3 1 6 4 7 10 14 13
样例输出
1 1 13
| 样例 | 解释说明 |
|---|---|
| 样例1 | 1表示是二叉搜索树前序遍历结果,1表示左侧地面呈现的伞坠数字值,13表示右侧地面呈现的伞坠数字值 |
数据范围
- 数组成员至少是1个
- 数组任意两个数字互不相同
- 最多1000个正整数
- 正整数值范围
题解
这道题目主要考察二叉搜索树和前序遍历的知识。
首先,我们需要了解什么是二叉搜索树:
- 二叉搜索树是一种特殊的二叉树,其左子树上所有节点的值都小于根节点的值
- 右子树上所有节点的值都大于根节点的值
- 左右子树也分别为二叉搜索树
前序遍历的特点是:根-左-右的访问顺序,即先访问根节点,再访问左子树,最后访问右子树。
题目分为两个部分:
- 判断给定序列是否为二叉搜索树的前序遍历结果
- 如果是,找出左右两侧的"伞坠"值;如果不是,返回"0 0 0"
对于第一个问题,我们可以通过递归的方式判断序列是否符合二叉搜索树的前序遍历特征:
- 序列的第一个元素是根节点
- 从第二个元素开始,找到第一个大于根节点的元素位置,这个位置之前的都是左子树节点
- 这个位置及之后的都是右子树节点
- 右子树的所有节点值都应该大于根节点值
- 递归判断左子树和右子树序列是否符合二叉搜索树的前序遍历
对于第二个问题,"伞坠"实际上指的是二叉树最底层最左和最右的叶子节点:
- 左伞坠:二叉树最后一层最左边的叶子节点
- 右伞坠:二叉树最后一层最右边的叶子节点
我们可以通过递归或迭代的方式构建二叉搜索树,然后找出左右伞坠节点。查找过程类似深度优先搜索,对于左伞坠,优先往左子树查找,如果左子树不存在再往右子树查找;对于右伞坠,优先往右子树查找,如果右子树不存在再往左子树查找。
算法的时间复杂度为O(n),其中n是序列的长度,我们需要遍历序列一次来构建树并找出伞坠值。空间复杂度也是O(n),用于存储递归调用栈和构建的二叉树。
对于给定的范围(最多1000个节点),这个复杂度是完全可以接受的。
参考代码
- Python
import sys
input = lambda:sys.stdin.readline().strip()
# 读取输入序列
pre_order = list(map(int, input().split()))
# 定义二叉树节点类
class TreeNode:
def __init__(self, val):
self.val = val # 节点值
self.left = None # 左子节点
self.right = None # 右子节点
# 判断是否是二叉搜索树的前序遍历结果,并构建树
def build_bst(start, end):
if start > end:
return None
# 根节点
root = TreeNode(pre_order[start])
# 找到第一个大于根节点的元素位置
i = start + 1
while i <= end and pre_order[i] < root.val:
i += 1
# 检查右子树的所有元素是否都大于根节点
j = i
while j <= end:
if pre_order[j] <= root.val:
return None # 不符合二叉搜索树特性
j += 1
# 递归构建左右子树
root.left = build_bst(start + 1, i - 1)
root.right = build_bst(i, end)
return root
# 查找左伞坠值
def find_left_drop(root, level):
if not root:
return 0
# 优先查找左子树
if root.left:
return find_left_drop(root.left, level + 1)
# 如果左子树不存在,检查是否是根节点
if level == 0:
return 0 # 根节点没有左子树,没有左伞坠
# 如果不是根节点且左子树不存在,检查右子树
if root.right:
return find_left_drop(root.right, level + 1)
# 如果左右子树都不存在,当前节点就是叶子节点,也就是左伞坠
return root.val
# 查找右伞坠值
def find_right_drop(root, level):
if not root:
return 0
# 优先查找右子树
if root.right:
return find_right_drop(root.right, level + 1)
# 如果右子树不存在,检查是否是根节点
if level == 0:
return 0 # 根节点没有右子树,没有右伞坠
# 如果不是根节点且右子树不存在,检查左子树
if root.left:
return find_right_drop(root.left, level + 1)
# 如果左右子树都不存在,当前节点就是叶子节点,也就是右伞坠
return root.val
# 构建二叉搜索树
root = build_bst(0, len(pre_order) - 1)
# 输出结果
if root:
left_drop = find_left_drop(root, 0)
right_drop = find_right_drop(root, 0)
print(f"1 {left_drop} {right_drop}")
else:
print("0 0 0")
- Cpp
#include <bits/stdc++.h>
using namespace std;
// 定义二叉树节点结构
struct Node {
int val; // 节点值
Node* left; /剩余60%内容,订阅专栏后可继续查看/也可单篇购买
本专栏收集并整理了一些刷题笔记