合法括号序列判断_另类加法_走方格的方案数

合法括号序列判断

合法括号序列判断

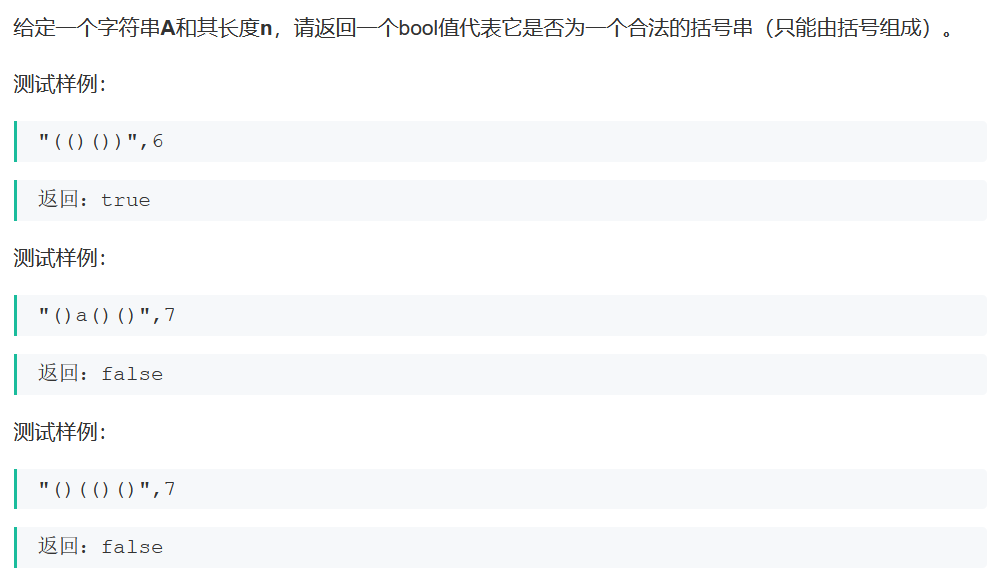
import java.util.*;

public class Parenthesis {
    public boolean chkParenthesis(String A, int n) {
        // write code here
        //根据题意,字符串只能由扩号组成!
        if(n%2==1){//字符长度为奇数,说明不匹配
            return false;
        }
        Stack<Character> stack = new Stack<>();
        for(int i = 0;i< n; i++){
            char ch = A.charAt(i);
            if(ch=='('){
                //左括号就入栈!
                stack.add(ch);
            }else if(ch==')'){
               //右括号,匹配出栈!
               if(stack.isEmpty()||stack.peek()==')'){
                   //如果栈空,或者栈顶值为 ')' 说明匹配失败!
                   return false;
               }else{
                   //匹配成功
                   stack.pop();
               }
            }else{
                //其他字符说明匹配失败!
              return false;
            }

        }
       if(stack.isEmpty()){
            return true;
        }
       return false;
    }
}

另类加法

另类加法

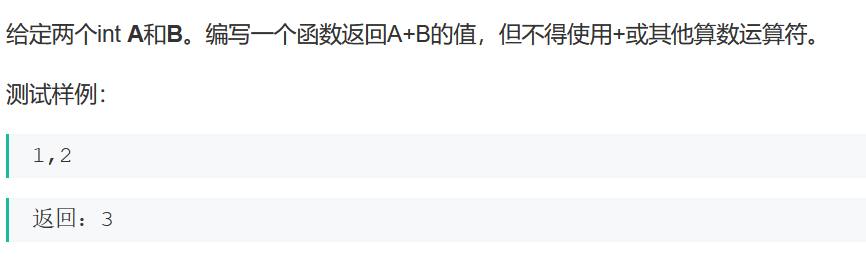
import java.util.*;
public class UnusualAdd {
    public int addAB(int A, int B) {
        // write code here
        // 两个数 异或(^)结果为两数之和 不考虑进位!!!
        // 两个数 按位与(&)后,左移1位结果为是否进位, 只考虑进位!
        // 例如: 3 + 2
        // 3  0011
        // 2  0010
        //sum = 0011^0010 = 0001
        //carry = (0011&0010)<<1 = 0100 
        //然后再将 sum 和carry 分别赋值给 A和B即可!
        // 知道 B == 0也就不用进位,此时sum 结果就为 A+B
        int sum = 0;
        int carry = 0;
        while(B!=0){
            sum = A^B;
            carry = (A&B)<<1;
            A = sum;
            B = carry;
        }
        return A;
    }
}

走方格的方案数

走方格的方案数

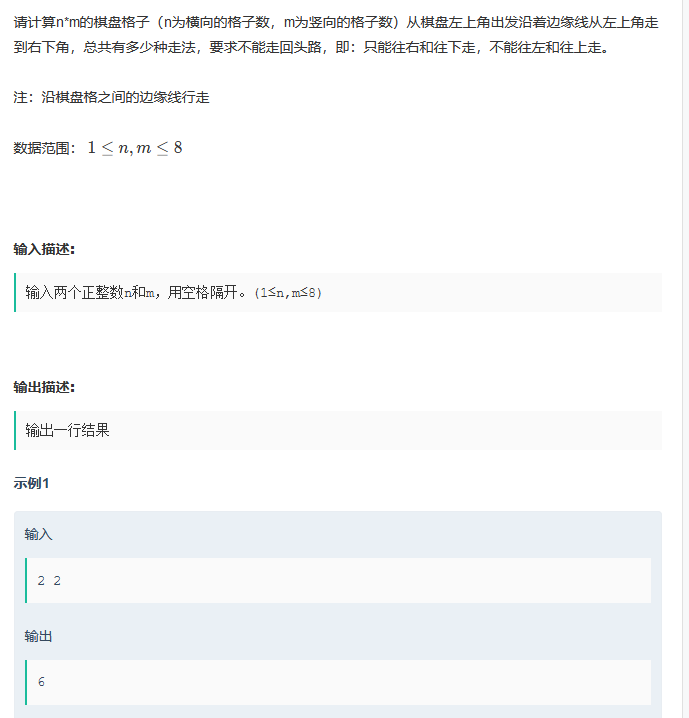
import java.util.*;
public class Main{
    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int m = sc.nextInt();
        int[][] array = new int[n+1][m+1];
        //dp动态规划
        //状态定义: 到达(i,j)位置的走法!
        //状态转移方程:f(i,j) = f(i-1,j) + f(i,j-1);
        //初始状态:f(i,0) = 1 ,f(0,j) = 1;
        //返回结果:f(n,m)!!!

        //初始化 
        for(int i = 0;i<=n;i++){
            array[i][0] = 1;
        }
         for(int i = 0;i<=m;i++){
            array[0][i] = 1;
        }
        for(int i = 1; i <= n;i++){
            for(int j = 1;j <= m;j++){
                array[i][j] = array[i-1][j] + array[i][j-1];
            }
        }
        System.out.println(array[n][m]);
    }
}